Features
Woodwinds
Departments
Csound Implementation of Physical Models of Woodwind Instruments
Josep Mª Comajuncosas Nebot
Introduction
Basic implementation
the reed
the clipping
routine
coupling the
reed with the bore
the bore
the tonehole
reflection filter
Csound minutiae
the player and the
instrument
integration scheme
filters and delay lines
legato notes : the dual
bore structure
recoding all the stuff with
Macros
MIDI and Score
implementations
Some working examples
The clarinet : single
reed cylindrical woodwind
Grallot : a double reed
clarinet
the tuning
problem
Future work
conical bores and
mouthpieces
defining playing
styles
Bibliography
Introduction
The motivations behind this work came
from an article I read a year ago in the Journal of New
Music Research, vol. 24 (1995): "Physical Models
of Wind Instruments : A Generalized Excitation Coupled
with a Modular Tube Simulation Platform" by Gijs
de Bruin and Maarten van Walstijn.
Later on I contacted Maarten at the
Edinbugh University and he helped me with this
implementation, giving details, suggestions and
improvements. I´m much indebted to his friendly
collaboration to make this project and this article
possible.
The extension to double reed instruments
is based on the work of Ana Barjau (Universitat
Politecnica from Barcelona) relating the modelling af the
Tenora, a catalan tenor shawn.
Most of the Csound implementation is
biased towards the clarinet by now, and most of the given
examples will be from my last clarinet model, which can
be found on my Csound page at
http://members.tripod.com/csound/
My aim is to build a nice collection of virtual woodwind instruments of great quality to use them in my Csound compositions. In this article I summarize the current progress of the implementation and two already functional models are presented : a clarinet and the Grallot (a sort of doublereed clarinet).
Basic implementation
the reed
One of the main differences between
this woodwind model and the ones implemented in the
Csound sources - from P. Cook´s Synthesis Toolkit
- is the simulation of the reed nonlinearity.
Instead of a memoryless nonlinearity
implemented as a lookup table, here a dynamic model of
the reed is employed, which takes into account air
inertia and reed beating.
The equations used to describe the reed
motion and the flow through the reed aperture are shown
here.
The reed is itself considered as a
harmonic oscillator driven below its resonance frequency,
that is, for cane reeds

which after some simplification and cosmetics becomes
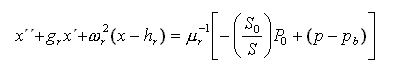
I refer you to the bibliography and the
Csound code for a complete description of all the
parameters involved. The Bernoully pressure (pb) takes an important role
in double reeds but is neglected in clarinet-type single
reeds.
Notice this equation assumes that the reed-lips
damping and stiffness is constant and equal to their
value with the reed at equilibrium. This simplification
seems to work well enough, but those parameters have a
decisive infuence on the timbre and the tuning of the
instrument and could be considered variable for
expressivity or fine tuning purposes.
The flow entering the reed as function
of the reed aperture and the pressure difference
between the mouth and the mouthpiece is assumed to obey
Backus equation for single reed instruments
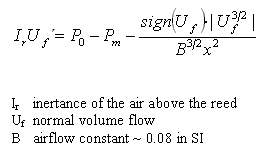
and a modified Backus equation for double reeds, taking into account the different reed geometry
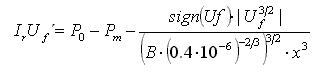
(0.4e-6 is the reed aperture in
equilibrium for a clarinet, the instrument in which
Backus measurements were done). I´ll possibly experiment
with another set of equations described in the revised
Nederveen´s thesis.
Those equations are solved in the time
domain using a custom integration scheme described later
in this article.
the clipping routine
Notice that at very small reed
apertures (when playing hard) the Backus equation is no
longer valid and can lead to large numerical errors. Also,
the reed aperture cannot go to zero as in a real
instrument. To overcome that problem several strategies
have been proposed, like desining different computing
zones according to the reed aperture.
A cheaper solution is proposed here. One
could truncate the reed aperture to an arbitrary small (but
not 0) value, but this produces very artificial overtones
(MP3). This is logical as we are hard clipping the
signal.
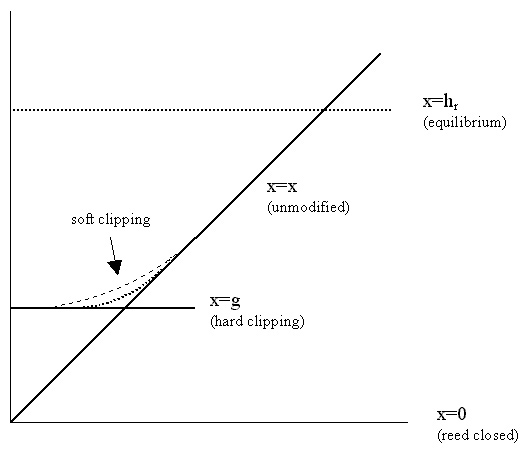
A soft clipping routine is preferred
instead. I first tried a tanh() function but it tended to
close the reed too much. As suggested by Maarten van
Walstijn, I implemented a new routine in which the
clipping function consists of two lines that are
interpolated by a circular segment. It has several
nice properties, like allowing gradually higher harmonic
richness at higher playing pressures (MP3),
allowing overblowing (MP3) and being parametrizable. This is vital
because the reed clipping has a strong effect on the
sound and makes possible a large variety of reeds and
playing styles. This clipping routine can be considered
as a phenomenological model of the reed curling up the
mouthpiece.
coupling the reed with the bore
To couple the reed with the bore one
must be able to compute the outgoing pressure (p right) which will
be the value injected into the waveguide, from the flow Ub and the ingoing pressure
(p left).
The total flow Ub coming into the bore equals the normal volume
flow Uf already
computed plus
an extra flow produced by the reed movement itself
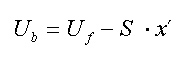
According to Nederveen this term
behaves like a virtual volume added to the mouthpiece
cavity and one has to compensate for it when computing
the total delay time of the waveguide.
We can now relate flow and pressure with
the well-known formula
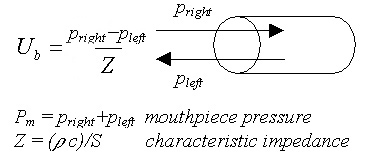
the bore
The bore is implemented as a recursive comb filter. Specifically, the current implementation is simple enough (i.e, a single cylindrical bore without a tonehole lattice) to allow a special implementation which makes use of a single waveguide of double length (half the wavelength of the desired note in the case of an open/closed cylinder) to simulate the upward and inward travelling waves. This method is similarly implemented in R. Cook´s woodwind and stringed instruments.
the tonehole reflection filter
Assuming that most of the radiation
coming out of the clarinet is due to the first open
tonehole, we can neglect the rest of the bore and derive
the reflectance and transmittance filters from a generic
clarinet tonehole and apply it to all pitches, as if the
clarinet was a sizeable cilinder with the tonehole at the
end of the bore.
Of course the subtle differences between
the clarinet pitches are lost, but as a first
approximation the result is acceptable.
The filter design routine has been
implemented in Matlab by Maarten van Walstijn and matches
the frequency and phase response of the theoretical
tonehole response according to D.Keefe´s tonehole models.
The frequency response of the reflection filter has a
lowpass shape with a cutoff frequency of about 1,5 kHz,
which agrees well with Keefe´s measurements.
The transmittance filter is derived by
performing a digital lowpass to highpass transformation
to the reflection filter.

The phase response of the refletance filter is taken into account when computing the total delay length, compensating for it in the main delay line.
The final bore structure as shown below includes the main waveguide together with the tonehole reflection filter and a fractional delay filter to fine tune the delay length. Notice that the transmittance filter is outside the feedback mechanism and thus could be parameterizable (for tone and brightness control) without undesired effects on the tuning (MP3)
Csound minutiae
the player and the instrument
As the aim is to accurately model an
instrument it is conceptually advisable to split the code
into 2 Csound instruments. The first one works as the
player, that is, it is activated at each new event and
sends the appropiate performance values (such as flow and
reed parameters, pitch, volume and so on) to the second
instrument.
The second one, which is left active
throughout the performance, is the implementation of the
model itself.
The communication between both instruments
is held via zak variables.
integration scheme
The system of equations describing the
reed motion and the air flow through it are integrated as
follows: first integrate the reed motion (2nd order ODE)
with the Euler method. Thus we will get the reed aperture.
Then integrate the Backus flow equation
with Euler again and solve the resulting first order
differential equation with the Newton-Rhapson iterative
method, initialising with the previous value obtained. No
more than 3 iterations seem to be necessary for
convergence.This last equation will give you the flow
coming into the bore.
All these equations are explicitely coded
in the orchestra, as there are not yet opcodes to
automatically perform such integrations. Some other
integration schemes could be experimented, but according
to the bibliography this is the one offering faster
convergence and better stability.
filters and delay lines
The filters employed to implement the tonehole (reflectance and transmission filters) are designed with Matlab as 1st or 2nd order sections and thus can be implemented in Csound with the biquad opcode. Though rather simple they approximate very well the actual tonehole response and allow an analytic computation of their phase delay, which is used to fine tune the instrument.
The fractional delay filter is implemented as a simple interpolator (a first order Lagrange interpolator) but I´ll soon implement it as a 3rd order FIR filter with the filter2 opcode, which should minimize the high frequency losses.
The delay line is implemented as a delayr/delaw pair, from where I extract the precise sample with the deltapn opcode. Notice a cubic interpolation could be possible without the explicit use of filter opcodes, making use of the new deltap3 opcode. I avoided it because I´m not sure if it is reliable enough.
legato notes : the dual bore structure
Because the woodwind is left active
during the performance, it is possible to deal with
legato notes quite easily.
The problem with the current
implementation is that the pitch is not determined by a
combination of open and closed holes, instead, one
changes the length of the main delay line simulating the
bore.
Changing the pitch in a legato fragment could be done by shortening or enlarging the bore like in a slide flute, but this glissando sounds unnatural and causes the volume to increase during the note transition.
The solution was to
implement a second bore running in parallel with the
first. At each new event the bore is switched with an
appropiate crossfade time. The crossfade is not linear
but sigmoidal, though the difference is subtle. The
result is not unlike the transition time needed to change
the fingering in a real instrument. 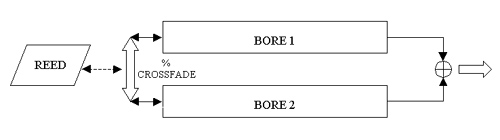
I found that the optimum transition time depends on the note frequency and the speed of the fragment to be played. If it is too low a glissando is heard and the note takes longer to oscillate at the expected amplitude, if too short, the abrupt transition will cause noticeable clicks.
recoding all the stuff with Macros
More recently I decided to recode the instruments making use of the new Macro functionality. Thus the woodwind is built in a modular way: reed + bore + tonehole. The reed itself, for example, also includes macro calls showing its internal structure : reed motion + clipping routine + flow equation. Hopefully the code is more readable this way. Also it makes it easy to change part of the code, to apply it to different designs and eventually to port all the stuff to C++ or viceversa (that´s what I´m actually doing with Maarten´s C++ implementation of the clarinet).
MIDI and Score implementations
Both a MIDI and a Score activated
orchestra will have the "instrument" identical,
but the "player" code will differ depending on
how the event is activated.
A Score implementation has the advantage
of knowing in advance the duration of the events, which
can be a criterium to choose the optimum playing
parameters.
A MIDI implementation is possible, however
the instrument is quite computationally intensive and
will demand a powerful machine to run in real time.
Notice also that the legato feature makes
it monophonic. Each new event is assumed to be the next
note of the melody. To play polyphonic sequences, simply
set different instrument pairs in the orchestra code,
taking care of the zak variables, and call them
accordingly.
Some working examples
The clarinet : single reed cylindrical woodwind
Usually the clarinet is a good
candidate to begin this kind of modeling, because of its
relative simplicity : a nearly cylindrical bore with a
small bell which can be neglected for most pitches, and a
single reed is much simpler to model than the saxophone´s.
The clarinet mouthpiece can also be neglected at a first
approximation without so much discrepancy as in the sax.
Notice that, similar to a real clarinet,
the model has a playing extension which is limited both
by the reed resonance frequency and especially by the
frequency cutoff of the tonehole filter. In other words:
it cannot reach higher pitches than the real instrument,
but there is no problem with lower ones.
After the appropriate corrections, the
instrument is surprisingly well tuned. A drawback is that
with the same input pressure higher notes sound pale and
dull, presumably because they would demand a higher lips
pressure, or better, using the 12th instead of the
fundamental tone. I´ll try to fix that soon.
| MIDIfied Clarinet (old code): orc & sco files in zip format |
| Clarinet (improved .sco version) : orc & sco files in zip forma |
Grallot : a double reed clarinet
This instrument is my first nearly
successful implementation of a double reed, which is far
more complicated because of the higher Bernoulli pressure
caused by the small reed apertures and the more
pronounced beating regime.
It is coupled to a cylindrical bore, which
is not common in the real doublereed instruments, usually
of conical shape.
The implementation is based on an older
code of my clarinet model, so it doesn´t yet include
macros and some other refinements. Think of it as a
clarinet with a double reed rudely attached to it.
the tuning problem
Despite taking into account all the
parameters infuencing the pitch -those related to the (frequency
dependent) phase delay caused by the tonehole reflectance
filter, the (constant) delay induced by the extra flow in
the reed motion equation, and the fractional delay
filters- the instrument can be completely out of
tune sometimes. This was notorius in my Grallot,
probably because I neglected some crucial parameters (or
there could even be a serious mistake somewhere !).
A way to overcome the problem and make the
instrument more responsible to the player reactions is to
couple its output to a pitch tracker, as I did in the Grallot.
The pitch tracker is implemented with the pitchamdf
opcode. It automatically readjusts the main delay
line lenght in order to get the desired pitch:
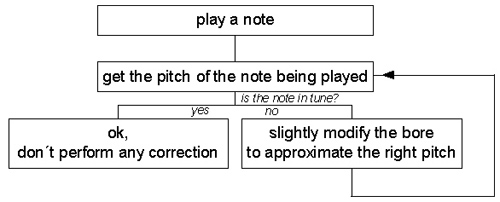
It is advisable to store a fairly good
approximation of the correction needed for all the pitch
range in a table to initialize the tracker with a good
value and minimize the initial glissando, otherwise it
will sound as much grotesque as my Grallot !
This routine is so robust that it even
kills the vibrato I added for more naturality. It would
be better either to have certain tolerance or even better,
deactivate the tracker once the right pitch has been
reached and no glissandos are expected.
A more physical behaviour could be to
change the pitch with the lips pressure, something the
real players do all the time.
| Grallot mp3 example Grallot orc & sco files in zip format |
Future work
conical bores and mouthpieces
Implementing piecewise conical
waveguides is the next step in the model, to be able to
design bores of arbitrary shape. It is well known that
implementing conical sections can lead to numerical
instabilities and Csound could not work wery well until
double precision is implemented.
Related to this a mouthpiece model would
be desirable for the clarinet, anticipating a much harder
work for the saxophone family.
Modelling a whole tonehole/register hole lattice might well be an exhausting experiment and I leave it for the future, as well as implementing the bell with the new Truncated IIR filters.
defining playing styles
Once you have a very
accurate woodwind instrument, sensitive to all the
playing parameters such as lips and mouth pressure, flow
pressure, fingerings, etc. how do you play such a beast
with a MIDI keyboard or even worse, with a numerical
Score written by hand?
A good woodwind model needs also a good
player, possibly a player model which should
automatically take some obvious decisions, such as the
optimum attack and pressure for each pitch (I´m already
working on this), and eventually store a palette of
standard playing styles like legato, non legato, stacatto,
hard, soft playing, crescendo notes, vibrato notes and so
on.
Some serious research is needed to "code"
someway these playing styles.
This way the instrument could be
reasonably playable even from a keyboard or an
algorithmic composition software, without the need of
capturing real live parameters from a performance.
Josep Mª Comajuncosas Nebot
september 1999 TOP
Bibliography
A. Barjau, J. Agulló: Calculation of the Starting Transients of a Double-reed Conical Woodwind. Acustica, vol.69 (1989)
A. H. Benade: Fundamentals of Musical Acoustics. Second edition. Dover publications, NY 1990.
Gijs de Bruin, Maarten van Walstijn: Physical Models of Wind Instruments : A Generalized Excitation Coupled with a Modular Tube Simulation Platform. Journal of New Music Research, vol. 24 (1995)
M. Pavageau: Synthèse d´un modèle physique d´anque double. Rapport du stage D.E.A. d´Acoustique Appliqué de l´Université du Maine. Septembre 1993
C. J. Nederveen: Acoustical Aspects of Woodwind Instruments.Revised edition. Northern Illinois University Press. DeKalb 1998
