Introduction
This article is about aspects of swing rhythm in Csound. The implementation of durations for straight and swing values in the score are discussed including various ratios. Ideas for improving swing rhythms in the score such as mathematical calculations inline, and score macros are demonstrated. Examples using the schedule and event opcodes to shift placement of swing rhythms in time are presented. Finally a brief description of groove templates is mentioned with ideas for how those might be further developed. Versions used for this article were Fedora 21, and Csound 6.03.
In [1] Roger Linn writes about introducing swing, as well as recording quantization in the LM-1 Drum Computer in 1979. While the historical period of the swing or big band era in jazz was during the 1930s and 40s, for many computer musicians Linn's technology introductions are of equal importance because they signal a method of calculating swing rhythmic values. Wesolowski [2]writes that the three variables of measurements of eighth note values, beat placement, and note dynamics contribute to the overall structure and functioning of swing rhythm.
I. Straight Eighths
Figure 1, below, shows an original jazz-like melody over the "Ja-Da" changes. The so called straight eighth notation for the eighth note rhythmic values of the melody consists of several groups of successive eighth note patterns punctuated by longer durations, and the sounding harmony, in the following audio example, is a simple block chord background of whole and half note values utilized to frame the 4/4 measures. The melody is provided as a sample for discussing aspects of swing, below.
 Figure 1. Straight eighth notes.
Figure 1. Straight eighth notes.
Audio Example1.mp3 is a Csound rendering of the straight eighth version of the melody with harmony. In Example1.csd, there are two STK instruments utilized in the orchestra. STKMoog gives a reedy quality, as a saxophone-like sound, while STKWurley provides a soft Wurlitzer electric piano background. You can download all the Csound swing examples shown in this article from the following link: Swing_exs.zip.
II. Swing Rhythm
Straight eighth note values, such as above, give way to a looser feeling in swing, usually of long and short patterns. A division of the quarter note into 2/3 and 1/3 divisions of triplets, or the dotted eighth and sixteenth note, are often used to indicate eighth note swing rhythm in music notation as shown below in Figure 2. Attempting to indicate the actual and precise notational values for an intricately performed rhythm, such as swing, instead of writing straight eighths or employing one of the notational conventions, can become difficult to read. Musicians generally prefer to experience, and learn to repeat the swing style of a piece of music by ear, so that their performance of the tune is familiar and recognizeable among listeners, but the rendering of it in notation is simple and straightforward.

Figure 2. Straight eighth and swing notation values.
In Example2.csd, a detailed swing rendering of the melody over the harmony is performed by adjusting each p2 and p3 start time and duration values in the score. The values were adjusted initially "by ear" to determine what sounds about right for a swing type feel for the melody under the given tempo. For long and short values, the values are 0.65 for the stretched eighth note and 0.35 for the shortened eigthth or snap portion of the swing value which fits within the overall duration of one quarter note. In the straight eighth Example1.mp3, the eighth note values are equal to 0.5 and 0.5 respectively. In the swing version there has been a 30% (0.65 - 0.5 = 0.15, and 0.15 divided by 0.5 = 0.3) alternating augmentation or diminution to the straight eighth note durations. Audio Example 2.mp3 is a swing rendering of the Csound score.
Collier & Collier write that the swing eighths ratio is not the 2:1 triplet, but ranges between 1.4 to 1 and 1.7 to 1, that is to say, the first of the swing pairs occupies, roughly, between 58% and 63% of the beat[3] . A good example of listening to a swing melody and live performance over the "Ja-Da" changes shown above is "Doxy" by Sonny Rollins.
Working with score durations, where for example the value of the quarter equals 1.0 in duration, we can program variations on swing rhythm as experiments to evaluate the results. If we divide the quarter or 1.0 in half for eighth notes or 0.5, then for swing, in terms of the augmented value, followed by the diminished value, we can substitute values which range from, for example, 0.60 and 0.40 to 0.75 and 0.25. Certain aspects of swing become clear by adjusting the rhythm and tempo values in the score. As tempos becomes slower, the small swing variation differences become more apparent. At faster tempos the swing variations are less apparent. At slower tempos, in order to have a swing feel, the rhythm augmentations tend to become "fatter" or larger. At faster tempos, the swing values can be quite diverse and still fit within the overall groove or "feel" of the music. As tempos become very fast, eighth notes tend to become more straight and can also be perceived as a group or flourish of notes leading towards longer note values. Collier & Collier have also observed, regarding the the triplet or 2:1 division of the quarter note, in terms of swing ratio, that it is tempo dependent, becoming more even as the tempo increases[3] .
Linn states that a 90 BPM swing groove will feel looser at 62% than at a perfect swing setting of 66%. And for straight 16th-note beats (no swing), a swing setting of 54% will loosen up the feel without it sounding like swing[1].
The basic unit of swing need not necessarily be long - short. For example the short - long - short rhythm or, 0.25, 0.5, 0.25 with swing applied, if the quarter is equal to 1.0 is often used. Duke Ellington's music is filled with an artful blend of various types of swing note values and patterns. Lindsay and Nordquist analyze several recordings by Duke Ellington for aspects of swing [4][5]. A piece which does not use any eighth notes at all, but is still in the swing style , is Neil Hefti's "Cute". Thus the long - short swing rhymic pair is probably the most common, but not necessarily the only one utilized to implement a swing style.
A macro aspect of swing rhythm, which has to do more with meter, is the shifting placement of groups of rhythms in relation to the underlying beat or pulse. Groups of rhythms, phrases, or an entire song may ebb and flow small amounts in relation to where the rhythms fall against the strong or regular pulses of the meter, as indicated below in figure 3. Gouyon writes about timing as short term changes in pulse, and tempo change as the overall long term change in the pulse [6]. The regular, underlying pulses may be only theoretical or agreed upon by consensus among the players and not actually heard, or they may be present in the percussion and/or rhythm instruments which help to maintain the pulse of the music and make it obvious. However, percussion and/or rhythm instruments may also adjust their time keeping by additions or subtractions to the theoretical underlying pulse, employing audible subtle changes of tempo to the meter.
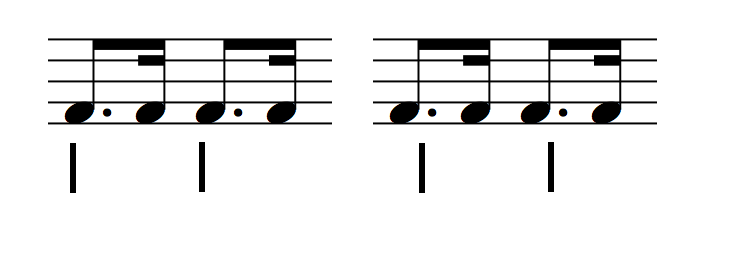
Figure 3. Shifting rhythmic groups over an underlying pulse.
The schedule opcode, seen in the code examples below, can be employed, by adjusting i-start, to simulate the ebb and flow small amounts of changes in relation to where the rhythms fall against the strong or regular pulses. Victor Lazzarini has written about this approach in Csound Journal in the article "Scoreless Csound" [7]. See the metro_phase.csd for an example of adjusting metronomic tempo pulses against a swing rhythm. Audio example3 below is an audio rendering of that .csd file.
III. Improving the Score
Various methods of Csound coding can be employed in the score in order to help create a swing feel. Example3.csd includes mathematical calculations inline within the score to arrive at an eighth note augmentation or diminution for each i-statement of the score file. The simple mathematical formulas of [.5 * 1.3] = .65 and [.5 * .7] = .35 are derived by 0.65 divided by 0.5 = 1.3, and 0.35 divided by 0.5 = 0.7. There is not much actual improvement here over Example2.csd, the manual or written out version which manually lists the augmentation and diminution values in the score, but it does make it visually clearer to see that it is the eighth note or 0.5 duration which is being adjusted to arrive at a swing feel for the melody.
i1 4.65 [.5 * .7] 7.05 100 0 i1 5 [.5 * 1.3] 8.02 100 0 i1 5.65 [.5 * .7] 7.10 100 0 i1 6 [.5 * 1.3] 8.00 100 0 i1 6.65 [.5 * .7] 7.08 100 0
In Example4.csd , score macros, named AUG and DIM respectively are created and applied to the score i-statements in place of the inline mathematical calculations used in Example3.csd to arrive at the swing values.
#define AUG #[.5*1.3]# #define DIM #[.5*.7]# i1 4.65 $DIM 7.05 100 0 i1 5 $AUG 8.02 100 0 i1 5.65 $DIM 7.10 100 0 i1 6 $AUG 8.00 100 0 i1 6.65 $DIM 7.08 100 0
In Example5.csd, macros and score preprocessing are applied to the score to further reduce the amount of text in the score. Although the score has become more concise, visually it is harder to determine the musicality of the swing values.
#define AUG #[.5*1.3]# #define DIM #[.5*.7]# i1 4.65 $DIM 7.05 100 0 i1 + $AUG 8.02 100 0 i1 . $DIM 7.10 100 0 i. . $AUG 8.00 100 0 i. . $DIM 7.08 100 0
Example6.csd. This is a scoreless example of a portion of the melody only, employing the use of global arrays which contain the pitch, rhythm, and amplitude values. In the examples above, the pitch and rhythm values had to be entered above as part of the i-statements of the score. In this example orchestra i-statements or init time statements initialize the data, and a simple oscillator instrument performs the values triggered by the schedule opcode.
<CsoundSynthesizer> <CsOptions> csound -s -d -+rtaudio=ALSA -odevaudio -b1024 -B16384 </CsOptions> <CsInstruments> sr = 44100 kr = 4410 ksmps = 10 nchnls = 2 0dbfs = 1 gipch[] fillarray 8.05, 9.02, 8.10, 9.00, 8.08, 8.07, 8.08, 8.10, 8.11, 9.02, 9.01, 9.00, 8.10, 8.09, 8.07, 8.09, 8.10, 9.00, 9.01 gidurs[] fillarray 0.35, 0.65, 0.35, 0.65, 0.35, 0.65, 0.35, 0.65, 2.35, 0.65, 0.35, 0.65, 0.35, 0.65, 1.0, 0.35, 0.65, 2.0, 2.0 giamp[] fillarray 0.35, 0.65, 0.35, 0.65, 0.35, 0.65, 0.35, 0.65, 1.0, 0.65, 0.35, 0.65, 0.35, 0.65, 1.0, 0.35, 0.65, 1.0, 1.0 i1 lenarray gipch iscale init 0.425 ;tempo scale icnt init 0 istart init 0 idur init 0 iamp init 0 ipch init 0 until icnt > 18 do idur = gidurs[icnt%i1] iamp = giamp[icnt%i1] ipch = gipch[icnt%i1] schedule 1,istart * iscale,idur * iscale, iamp, ipch istart = istart + idur icnt += 1 od instr 1 asig oscili p4, cpspch(p5) outs asig, asig endin </CsInstruments> </CsoundSynthesizer>
Example7.csd is a final scoreless example including melody and harmony, employing global arrays and the use of the schedule and event opcodes to trigger the STK instruments.
<CsoundSynthesizer>
<CsOptions>
csound -s -d -+rtaudio=ALSA -odevaudio -b1024 -B16384
</CsOptions>
<CsInstruments>
sr = 44100
kr = 4410
ksmps = 10
nchnls = 2
0dbfs = 1
;global var as percent
giaug init 1.3
gidim init 0.7
;global arrays
gipch[] fillarray 7.05, 8.02, 7.10, 8.00, 7.08, 7.07, 7.08, 7.10, 7.11, 8.02, 8.01, 8.00, 7.10, 7.09, 7.07, 7.09, 7.10, 8.00, 8.01
gidurs[] fillarray (.5 * gidim), (.5 * giaug), (.5 * gidim), (.5 * giaug), (.5 * gidim), (.5 * giaug), (.5 * gidim), (.5 * giaug), 3.35, (.5 * giaug), (.5 * gidim), (.5 * giaug), (.5 * gidim), (.5 * giaug), 1.0, (.5 * gidim), (.5 * giaug), 2.0, 2.0
gkchord[] fillarray 7.10, 8.02, 8.05, 8.07, \
7.08, 8.00, 8.03, 8.05, \
7.07, 7.11, 8.02, 8.04, \
7.07, 7.11, 8.02, 8.04, \
7.10, 8.00, 8.04, 8.07, \
7.09, 8.00, 8.03, 8.05, \
7.10, 8.02, 8.05, 7.10, \
7.09, 8.01, 8.03, 8.05
i1 lenarray gipch
iscale init 0.425 ;tempo scale
icnt init 0
istart init 0
idur init 0
ipch init 0
until icnt > 18 do ;until duration of the array
idur = gidurs[icnt%i1]
ipch = gipch[icnt%i1]
schedule 1,istart * iscale,idur * iscale, ipch, 100, 0 ;melody inst
schedule 2.1, 0.15 ,18 ;this one plays inst 2 for the duration of 18 ;harmony inst
istart = istart + idur
icnt += 1
od
instr 1 ;Melody (swing) instrument
ifrq = p4
kv1 line p5, p3, p6 ;filter Q
asig STKMoog cpspch(ifrq), 1, 2,kv1, 4, 120, 11, 40, 1, 1, 128, 120
asig = asig * .1
outs asig, asig
endin
instr 2 ;event trigger instrument 3 harmony
iscale init 0.425 ;tempo scale (match mel inst 1)
idur = 2.0 * iscale
kcnt init 0
i1 lenarray gkchord
if metro(1/idur) == 1 then
event "i",3,0,idur, gkchord[kcnt], 75, 0, 20
event "i",3,0,idur, gkchord[kcnt+1], 75, 0, 20
event "i",3,0,idur, gkchord[kcnt+2], 75, 0, 20
event "i",3,0,idur, gkchord[kcnt+3], 75, 0, 20
kcnt = (kcnt == i1 ? 0 : kcnt+4) ;count by 4
endif
endin
instr 3 ;harmony
ifrq = p4
kv1 line p5, p3, p6 ;(FM) Modulator Index One
kv3 = p7
asig STKWurley cpspch(p4), 0.01, 2,kv1, 4, 10, 11, kv3, 1, 30, 128, 75
outs asig, asig
endin
</CsInstruments>
</CsoundSynthesizer>
IV. Grooves
Grooves or groove templates are another aspect of rhythm often associated with swing, rhythm quantization, beat extraction, and hardware drum machines or software plugins. The idea of swinging together as an ensemble, or as a smaller choir of instruments or voices within the whole ensemble, can be facilitated by the application of groove templates. Because we are working on the code level with numbers for start times, durations, and percentages, essentially, we have the needed groove data easily available to us for use in additional instrument score note lists, or array contents.
For example a portion of Csound's console output derived from the start of Example2.csd, above, is shown below where the start times, end times, accumulated durations, and channel amplitudes are representative of the information sent to Csound via the score portion of the .csd file. (The console output below was adjusted to 60 bpm for clarity, while in Example2.csd, the tempo is 152 bpm (t 0 152), and the actual console output will appear different based on the faster tempo.)
B 0.000 .. 4.650 T 4.650 TT 4.650 M: 0.00000 0.00000 B 4.650 .. 5.000 T 5.000 TT 5.000 M: 0.08928 0.08928 B 5.000 .. 5.650 T 5.650 TT 5.650 M: 0.21693 0.21693 B 5.650 .. 6.000 T 6.000 TT 6.000 M: 0.17548 0.17548 B 6.000 .. 6.650 T 6.650 TT 6.650 M: 0.12450 0.12450 B 6.650 .. 7.000 T 7.000 TT 7.000 M: 0.09974 0.09974 B 7.000 .. 7.650 T 7.650 TT 7.650 M: 0.24148 0.24148 B 7.650 .. 8.000 T 8.000 TT 8.000 M: 0.15668 0.15668 B 8.000 .. 8.650 T 8.650 TT 8.650 M: 0.11987 0.11987 B 8.650 .. 9.000 T 9.000 TT 9.000 M: 0.09015 0.09015
The Csound time and tempo family of opcodes also can also provide more detailed output, from audio or score files, useful for developing and applying groove templates which can be applied to additional instruments within a swing texture to help create an overall groove effect. For example the times opcode, which reads absolute time in seconds, provides data which is similar to console output. The following code snippet is borrowed from times_complex.csd by Joachim Heintz and Rory Walsh from The Csound Cannonical Reference Manual [8].
iDur = p3 kTime times prints "start = %f, duration = %f\n", i(kTime), iDur
From Example6.csd, or Example7.csd above, durations from global arrays (gidurs[ ]) are employed as idur of the schedule opcode. For additional voices to a texture, such as percussion or bass, it can be seen that slightly adjusting the start time of the schedule opcode (istart) and/or adjusting the percentages applied to the indiviudal durations, can also help provide variations in the groove feel for the individual voices.
V. Conclusion
Much more work could be done with MIDI and grooves. Since this article is not about MIDI, the work with MIDI was left undone in this current article. There is also much which could be done to demonstrate applications of timing templates or quantization maps for grooves [9]. Of further interest for making computer music is the idea of asynchronus aspects of voice parts within a texture using the schedule opcode to affect timing or shifting of patterns ahead or behind a pulse. Swing is more than algorithms controlling synchronicitiy among the parts; it involves the spontaneous implementation of a style which is hard to predict and completely replicate as an algorithm. However certain aspects of code to replicate swing rhythm may provide information for making small adjustements to timing which can possibly help create listener interest and include additional variety for computer music.
References
[1]Attack Magazine. (2015). "Roger Linn On Swing, Groove & The Magic Of The MPC'S Timing" [Online]. Available: http://www.attackmagazine.com/features/roger-linn-swing-groove-magic-mpc-timing/ [Accessed May 23, 2015].
[2]Brian C. Wesolowski, "Testing a Model of Jazz Rhythm: Validating a Microstructural Swing Paradigm" [Online], PhD Dissertation, University of Miami, Coral Gables, FL., 2012. Available: http://scholarlyrepository.miami.edu/cgi/viewcontent.cgi?article=1747&context=oa_dissertations [Accessed May 23, 2015].
[3]Geoffrey L. Collier and James Lincoln Collier, (2002, The Regents Of The University Of California) "A Study of Timing in Two Louis Armstrong Solos," Music Perception [Online], Spring 2002, Vol 19, No. 3, 463-483. Available: http://rhythmcoglab.coursepress.yale.edu/wp-content/uploads/sites/5/2014/09/CollierCollier_2002_A-study-of-timing-in-two-Louis-Armstrong-solos.pdf [Accessed May 24, 2015].
[4]Kenneth A. Lindsay and Peter R. Nordquist, " A technical look at swing rhythm in music," Acoustical Society of America 120, 3005 (2006).
[5]Kenneth A. Lindsay and Peter R. Nordquist, (2007). "Pulse and Swing: Quantitive Analysis of Hierarchical Structure in Swing Rhythm," [Online]. Available: http://www.tlafx.com/Papers/JASA07_LindsayNordquist.pdf [Accessed May 24, 2015].
[6]Fabien Gouyon, "A computational approach to rhythm description--Audio features for the computation of rhythm periodicity functions and their use in tempo induction and music content processing" [Online], PhD Thesis, Universitat Pompeu Fabra, 2005. Available: http://mtg.upf.edu/node/440 [Accessed May 24, 2015].
[7]Victor Lazzarini, (2014). "Scoreless Csound," Csound Journal [Online], Issue 20, October 22, 2014. Available: http://csoundjournal.com/issue20/scoreless.html [Accessed May 24, 2015].
[8] Barry Vercoe et Al., (2005). "times," The Canonical Csound Reference Manual. [Online] Available: http://www.csounds.com/manual/html/times.html [Accessed May 23, 2015].
[9]Simon Price, (2003). "Extracting Tempo/Timing From A Recording," Sound On Sound [Online], September 2003. Available: http://www.soundonsound.com/sos/sep03/articles/protoolsnotes.htm [Accessed May 24, 2015].
Discography
Sonny Rollins. (Released 2011). Doxy. On Sonny Rollins [4-disc CD set]. Ashbourne Co. Meath, Ireland: Membran Music Ltd. (Recorded January 30, 1953)
Count Basie. (Reissue 1970). Cute. On Basie Plays Hefti [Vinyl, LP, Album]. New York, N.Y.: EMUS-ES 120003. (Recorded 1953)
Louis Armstrong & Duke Ellington. (Resissue 1990). Cotton Tail, Black and Tan Fantasy, Mood Indigo, etc. On The Complete Louis Armstrong & Duke Ellinton Sessions. [CD]. New York, N.Y.: Roulette Jazz CDP 7 93844 2.(Recording date 1961)