Introduction
This article will take two well known examples of visual curiosities and consider their application as event generating modules in Csound. The visual kinetic systems considered are noteworthy on account of the unexpected patterns that arise during their activity. The aim is to construct musical analogues of these systems that can similarly evoke unexpected patterns. The examples provided will make use of the Csound front-end "Cabbage" [1] to confirm the mathematical rendering of the visual analogues and also to better facilitate user interaction and exploration, but these Cabbage visualisations and interfaces could easily be detached, making the examples front-end independent. All of the examples can be downloaded as a zip archive here.
I. The Stroboscopic Effect
Description
Analogue moving film works by taking a sequence of still images, which when played back at the same rate as that when taken, fool the eye and the brain into thinking that it is observing a moving image. In the early days of Hollywood the standard of 24 frames per second was established, not only because this rate is just about adequate for sustaining the illusion, but also as going much higher would have placed excessive technical strains on the equipment as well as increasing the amount, and therefore cost, of film stock required.
As Hollywood began its fascination with recreating the old West of the 1800s, a problem quickly became apparent when trying to film revolving wagon wheels in that they would appear to be moving too slowly, not at all, or even backwards. This popularly became known as "the wagon wheel effect"[2], but more generically should be referred to as the "stroboscopic effect". To understand the reason for this, first imagine a wagon wheel with a single spoke rotating about its centre once every second (Figure 1). If we tried to film this movement at a single frame per second each image would be identical therefore no movement would be captured. If we increased the rate very slightly, then the object would not quite have completed its rotation by the time of the second image, and so on continuing into the subsequent frames. In this case the object would appear to be rotating very slowly in the opposite direction to that of its actual travel. Decreasing the frame rate would result is very slow movement in the actual direction of travel. Of course film does not run at 1 frame per second but neither does a wagon wheel have to rotate a full 360 degrees in order to exhibit similarity. A wheel with just 2 spokes (Figure 1) repeats its appearance twice within every full rotation, or every 180 degrees; a wheel with 4 spokes repeats 4 times or every 90 degrees; 8 spokes repeats 8 times or every 45 degrees and so on. Increasing the number of instances of visual similarity in a rotation allows us to increase the frame rate while achieving the same anomaly. To derive the frame rate required to freeze motion we can apply the following equation:
where F is frames-per-second, R is the rate of rotation and N is the number of equally spaced spokes. From this we can deduce that a wheel with 16 spokes filmed at 24 fps will only need to rotate at 1.5 Hz in order to appear motionless (or multiples thereof: 3 Hz, 4.5 Hz etc.). An 8 spoked wheel will require a rotation of 3 Hz (or 6 Hz, 9 Hz etc.).
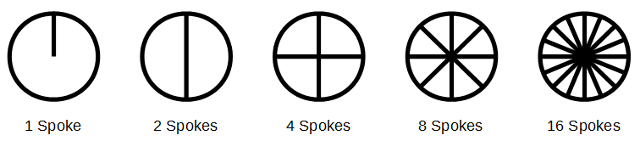
Figure 1. Wheels with varying numbers of equally spaced spokes.
Example01.csd employs the Csound front-end Cabbage to permit the user to explore the visual consequences of various rotational speeds and frame rates upon a spinning 8 spoked wheel. It should be noted that Cabbage is not really intended for the creation of animations of this sort so we are pushing it to its limit in this respect. For the best results give guirefresh() in the Cabbage code block a low value and also keep ksmps low. "Frames" are created using a metro, the output of which dictates when the Cabbage widgets for the spokes will be redrawn. The rotation of the wheel derives from a single phasor, the phases (and therefore rotations) of the various spokes being derived from this single phasor. Spokes are created using diameter chords and are therefore created in pairs. This example produces no sound.
; Example01.csd
<Cabbage>
form size(300,200), guirefresh(8), text("Wagon Wheel")
image bounds(100, 40,100,100), shape("ellipse"), colour(0,0,0,0), outlinethickness(3)
image bounds(100,90,100,4), identchannel("spoke1"), shape("rounded")
image bounds(100,90,100,4), identchannel("spoke2"), shape("rounded")
image bounds(100,90,100,4), identchannel("spoke3"), shape("rounded")
image bounds(100,90,100,4), identchannel("spoke4"), shape("rounded")
numberbox bounds( 0,170,150,30), text("Freq. of Rotation"), range(0,5,1,1,0.01), channel("freq")
numberbox bounds(150,170,150,30), text("Frames Per Second"), range(1,64,8.5,1,0.01), channel("FPS")
</Cabbage>
<CsoundSynthesizer>
<CsOptions>
-n
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 16
nchnls = 2
0dbfs = 1
instr 1
kfreq chnget "freq" ; read in Cabbage widgets
kFPS chnget "FPS"
gkRefresh metro kFPS ; refresh rate
kphs1 phasor kfreq ; phase vector defining the rotation of the wheel
if gkRefresh==1 then ; only update with a gkRefresh trigger, i.e. a frame
kphs2 wrap kphs1+0.125,0,1 ; second radius
kphs3 wrap kphs1+0.25,0,1 ; third radius
kphs4 wrap kphs1+0.375,0,1 ; fourth radius
Smsg sprintfk "rotate(%f,50,2)",2 * $M_PI * kphs1 ; create string
chnset Smsg, "spoke1" ; send string to widget
Smsg sprintfk "rotate(%f,50,2)",2 * $M_PI * kphs2
chnset Smsg, "spoke2"
Smsg sprintfk "rotate(%f,50,2)",2 * $M_PI * kphs3
chnset Smsg, "spoke3"
Smsg sprintfk "rotate(%f,50,2)",2 * $M_PI * kphs4
chnset Smsg, "spoke4"
endin
</CsInstruments>
<CsScore>
i 1 0 3600
</CsScore>
</CsoundSynthesizer>
For a given rotational frequency, the maximum rate of frames per second that will freeze motion will be eight times the rotation frequency. For a rotational frequency of 1 Hz, 8 frames per second will freeze motion as will halves of that value thereof (4, 2, 1 etc.). Transferring these visual results to (or mirroring them in) the creation of sound within Csound should prove relatively straightforward.
If we jettison the visual implementation and consider a purely sonic approach, we can periodically sample the phase vector and hold this value until the next sample is taken; this technique is commonly referred to as "sample-and-hold". This is something that is easy to construct from basic elements in Csound, but for which there exists a ready-made opcode called samphold. The following example takes the phase vector of the wagon wheel and interprets it as the pitch of an oscillator. This vector undergoes a reiterating sample-and-hold procedure and the result is used in defining the frequency of the oscillator. Just two controls are used: "Phase Rate", the frequency of the phase vector which is equivalent to the "Freq. of Rotation" from the previous example, and "S&H Rate" which is equivalent to "Frames per Second". Values can be changed by either spinning the encoders or by typing directly into the number boxes. Notions of freezing or reversing motion are transmuted into holding the pitch of the oscillator steady or forcing it to exhibit a descending scale but we will probably become more interested in other, less linear patterns that can be found.
; Example02.csd
<Cabbage>
form size(350,100), caption("Basic Stroboscopic Effect")
numberbox bounds( 10, 5,70, 30), range(-1000,1000,15.777-,1,0.0001), channel("PhsRate"), text("Phase Rate")
numberbox bounds( 90, 5,70, 30), range(0,1000,6,1,0.0001), channel("SHrate"), text("S&H.Rate")
</Cabbage>
<CsoundSynthesizer>
<CsOptions>
-n -dm0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 16
nchnls = 2
0dbfs = 1
instr 1
kPhsRate chnget "PhsRate"
kSHrate chnget "SHrate"
kSHTrig metro kSHrate ; train of triggers
aphs phasor kPhsRate ; a phase vector moving from 0 - 1
aoct samphold aphs + 7, kSHTrig ; repeatedly sample-and-hold phasor
asig poscil 0.2, cpsoct(aoct) ; sonify samp&hold signal
outs asig, asig
endin
</CsInstruments>
<CsScore>
i 1 0 3600
</CsScore>
</CsoundSynthesizer>
Figure 2 below illustrates the basic transformation of a frequency phase vector with a negative frequency. State (i) represents the untransformed function, or a rate of sample-and-hold equal to the sample rate. States (ii) and (iii) illustrate the increasing quantisation resulting from lower rates of sample-and-hold. As both the frequencies of the phasor and of the sample-and-hold share a common factor, simple periodicity is exhibited at the same frequency as the phasor. If the frequency of the sample-and-hold was lower than that of the phasor (but still with a shared common factor), then the resultant periodicity would be equal to the frequency of the sample-and-hold.

Figure 2. Sample and hold.
If the two frequencies do not share a common factor, then precise periodicity will not occur in the resultant function, as illustrated by Figure 3.
Figure 3. Non integer ratio sample-and-hold.
We can refine the sound produced somewhat by enveloping each step of the sample-and-hold process so that they become more like notes than mere temporal quantisations of a continuous function. We do not need to limit ourselves to using an input function that describes the cyclical phase vector of a rotation, we can explore other waveforms. The following example builds on the previous one by adding these refinements. The user can select between a sawtooth, a sine and a half-sine as input functions. The input function can also be DC shifted and its range can be scaled. The phase vector is now referred to as an input LFO.
; Example03.csd
<Cabbage>
form size(350,100), caption("Stroboscopic Effect")
button bounds( 10, 5,60, 30), text("Off","On"), channel("OnOff")
line bounds( 78, 0, 1,100)
numberbox bounds( 90, 5,70, 30), range(-1000,1000,15.777-,1,0.0001), channel("LFOrate"), text("LFO.Rate")
combobox bounds(165,18,70, 20), text("saw","sine","half-sine"), channel("wave")
numberbox bounds( 90,50,70, 30), range(0,6,1,1,0.01), channel("LFOrange"), text("LFO.Range")
numberbox bounds(165,50,70, 30), range(4,12,8,1,0.01), channel("LFOoffset"), text("LFO.Offset")
line bounds(243, 0, 1,100)
numberbox bounds(255, 5,70, 30), range(0,1000,6,1,0.0001), channel("SHrate"), text("S&H.Rate")
</Cabbage>
<CsoundSynthesizer>
<CsOptions>
-n -dm0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 16
nchnls = 2
0dbfs = 1
giwave ftgen 0,0,4097,10,1,0,0.2,0,0,0.05,0,0,0,0,0.01,0,0,0,0,0.001
gilfo1 ftgen 0,0,4097,7,0,4096,1 ; sawtooth up
gilfo2 ftgen 0,0,4097,19,1,1,0,1 ; sine wave shifted into the positive domain only
gilfo3 ftgen 0,0,4097,9,0.5,1,0 ; half-sine
instr 1
; read in widgets
kOnOff chnget "OnOff"
gkLFOrate chnget "LFOrate"
gkLFOrange chnget "LFOrange"
gkLFOoffset chnget "LFOoffset"
gkSHrate chnget "SHrate"
gkwave chnget "wave"
; turn instr 2 on and off
if trigger(kOnOff,0.5,0)==1 then
event "i",2,0,-1
elseif trigger(kOnOff,0.5,1)==1 then
turnoff2 2,0,0
endif
endin
instr 2 ;SAMPLE AND HOLD NOTE SEQUENCER
aoct oscilikt gkLFOrange, gkLFOrate, gilfo1+gkwave-1
kSHTrig metro gkSHrate
if kSHTrig==1 then
reinit RESTART_ENVELOPE
endif
RESTART_ENVELOPE:
aenv expseg 1,0.7,0.001,1,0.001
rireturn
aenv butlp aenv, 200 ; smooth envelope interruptions
aoct samphold aoct + gkLFOoffset, kSHTrig
asig poscil 0.2*aenv, cpsoct(aoct), giwave
asig butlp asig,8000*aenv
outs asig, asig
endin
</CsInstruments>
<CsScore>
i 1 0 3600
</CsScore>
</CsoundSynthesizer>
This technique’s ability to generate unexpected patterns—that can themselves be continually evolving depending on the LFO rate and sample-and-hold rates we choose—tempts us to explore the results when sonified using different non-pitched sounds. We can replace our continuous function with a sequence of drums sounds—each of the spokes of the wagon wheel representing a different drum sound if you like—and thereby create a drum rhythm generator. This is implemented in the next example which also combines a second LFO input which is used to define amplitude. This means that an amplitude emphasis pattern is created which cycles independently to the one used to define what sound is to be played. The first LFO (triangle wave shaped) when sampled will choose one from six possible sounds: kick drum, rim-shot, snare, closed hi-hat, open hi-hat and tambourine. The methods used to produce these sounds are not the subject of this article so are not discussed here. The second LFO, used to define the amplitude emphasis pattern, employs a simple square wave meaning that dynamics are binary: sounds are either accented or unaccented. This accenting LFO, if set to a different frequency than that of the sound selecting LFO, can undermine the repetitiveness of the basic pattern by adding subtle aperiodic variations in emphasis. By adding additional LFO functions—each with a different frequency value—to control additional sound attributes, we can add further layers of aperiodicity while the underlying periodicity of the sound selection LFO remains constant.
; Example04.csd
<Cabbage>
form size(350,100), caption("Strobe Drum Patterns")
button bounds( 10,10,60,30), text("Off","On"), channel("OnOff")
numberbox bounds( 80, 5,70,30), range(0,1000,8,1,0.0001), channel("SHrate"), text("S&H.Rate")
numberbox bounds(160, 5,70,30), range(0,1000,11.125,1,0.0001), channel("LFOrate"), text("LFO.Rate")
numberbox bounds(160,40,70,30), range(0,1000,17,1,0.0001), channel("LFOrate2"), text("LFO.Rate 2")
</Cabbage>
<CsoundSynthesizer>
<CsOptions>
-n -dm0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 16
nchnls = 2
0dbfs = 1
giSawDn ftgen 0,0,4097,7,1,4096,0
giTri ftgen 0,0,4097,7,0,2048,1,2048,0
giSqu ftgen 0,0,4097,7,1,2048,1,0,0,2048,0
instr 1
; read in widgets
kOnOff chnget "OnOff"
gkSHrate chnget "SHrate"
gkLFOrate chnget "LFOrate"
gkLFOrate2 chnget "LFOrate2"
; turn instr 2 on and off
if trigger(kOnOff,0.5,0)==1 then
event "i",2,0,-1
elseif trigger(kOnOff,0.5,1)==1 then
turnoff2 2,0,0
endif
endin
instr 2 ; sample-and-hold drum pattern generator
ktrig metro gkSHrate
anum poscil3 5.999, gkLFOrate, giTri
anum samphold anum + 3, ktrig
knum downsamp anum
aamp poscil3 1, gkLFOrate2, giSqu
aamp samphold (aamp*0.7) + 0.3, ktrig
kamp downsamp aamp
schedkwhen ktrig,0,0,int(knum),0,0.1,kamp
endin
; kick drum
gicos ftgen 0,0,131072,11,1
instr 3
kmul transeg 0.2,p3*0.5,-15,0.01, p3*0.5,0,0
kbend transeg 0.5,1.2,-4, 0,1,0,0
asig gbuzz 0.5,50*semitone(kbend),20,1,kmul,gicos
aenv transeg 1,p3-0.004,-6,0
aatt linseg 0,0.004,1
asig = asig*aenv*aatt
aenv linseg 1,0.07,0
acps expsega 400,0.07,0.001,1,0.001
aimp oscili aenv,acps*octave(0.25)
aBD = ((asig*0.5)+(aimp*0.35))*p4
outs aBD, aBD
endin
; rim shot
giTR808RimShot ftgenonce 0,0,1024,10, 0.971,0.269,0.041,0.054,0.011,0.013,0.08,0.0065,0.005,0.004,0.003,0.003,0.002,0.002,0.002,0.002,0.002,0.001,0.001,0.001,0.001,0.001,0.002,0.001,0.001 ;WAVEFORM FOR TR808 RIMSHOT
instr 4
idur = 0.027
p3 limit idur,0.1,10
aenv1 expsega 1,idur,0.001,1,0.001
ifrq1 = 1700
aring oscili 1,ifrq1,giTR808RimShot,0
aring butbp aring,ifrq1,ifrq1*8
aring = aring*(aenv1-0.001)*0.5
anoise noise 1,0
aenv2 expsega 1, 0.002, 0.8, 0.005, 0.5, idur-0.002-0.005, 0.0001, 1, 0.0001
anoise buthp anoise,800
kcf expseg 4000,p3,20
anoise butlp anoise,kcf
anoise = anoise*(aenv2-0.001)
amix = (aring+anoise)*0.8*p4
outs amix,amix
endin
; snare
instr 5
ifrq = 342
iNseDur = 0.3
iPchDur = 0.1
p3 = iNseDur
aenv1 expseg 1,iPchDur,0.0001,p3-iPchDur,0.0001
apitch1 oscili 1,ifrq
apitch2 oscili 0.25,ifrq*0.5
apitch = (apitch1+apitch2)*0.75
aenv2 expon 1,p3,0.0005
anoise noise 0.75,0
anoise butbp anoise,10000,10000
anoise buthp anoise,1000
kcf expseg 5000,0.1,3000,p3-0.2,3000
anoise butlp anoise,kcf
amix = ((apitch*aenv1)+(anoise*aenv2))*p4
outs amix,amix
endin
; closed hi-hat
instr 6
iactive active p1+1
if iactive>0 then
turnoff2 p1+1,0,0
endif
kFrq1 = 296
kFrq2 = 285
kFrq3 = 365
kFrq4 = 348
kFrq5 = 420
kFrq6 = 835
idur = 0.088
p3 limit idur,0.1,10
aenv expsega 1,idur,0.001,1,0.001
ipw = 0.25
a1 vco2 0.5,kFrq1,2,ipw
a2 vco2 0.5,kFrq2,2,ipw
a3 vco2 0.5,kFrq3,2,ipw
a4 vco2 0.5,kFrq4,2,ipw
a5 vco2 0.5,kFrq5,2,ipw
a6 vco2 0.5,kFrq6,2,ipw
amix sum a1,a2,a3,a4,a5,a6
amix reson amix,5000,5000,1
amix buthp amix,5000
amix buthp amix,5000
amix = amix*aenv
anoise noise 0.8,0
aenv expsega 1,idur,0.001,1,0.001
kcf expseg 20000,0.7,9000,idur-0.1,9000
anoise butlp anoise,kcf
anoise buthp anoise,8000
anoise = anoise*aenv
amix = (amix+anoise)*0.55*p4
outs amix,amix
endin
; open hi-hat
instr 7
kFrq1 = 296
kFrq2 = 285
kFrq3 = 365
kFrq4 = 348
kFrq5 = 420
kFrq6 = 835
p3 = 0.5
aenv linseg 1,p3-0.05,0.1,0.05,0
ipw = 0.25
a1 vco2 0.5,kFrq1,2,ipw
a2 vco2 0.5,kFrq2,2,ipw
a3 vco2 0.5,kFrq3,2,ipw
a4 vco2 0.5,kFrq4,2,ipw
a5 vco2 0.5,kFrq5,2,ipw
a6 vco2 0.5,kFrq6,2,ipw
amix sum a1,a2,a3,a4,a5,a6
amix reson amix,5000,5000,1
amix buthp amix,5000
amix buthp amix,5000
amix = amix*aenv*p4
anoise noise 0.8,0
aenv linseg 1,p3-0.05,0.1,0.05,0
kcf expseg 20000,0.7,9000,p3-0.1,9000
anoise butlp anoise,kcf
anoise buthp anoise,8000
anoise = anoise*aenv
amix = (amix+anoise)*0.3*p4
outs amix,amix
endin
; tambourine
instr 8
p3 = 0.5
asig tambourine 0.3*p4, 0.01, 32, 0.47, 0, 2300, 5600, 8000
outs asig, asig
endin
</CsInstruments>
<CsScore>
i 1 0 [3600*24*365]
</CsScore>
</CsoundSynthesizer>
Another approach, and one which provides better code economy, sends data retrieved from arrays using a pointer derived from the LFO/sample-and-hold to a single instrument. The following example sends values for stiffness and duration to an instrument generating sound using the barmodel opcode.
; Example05.csd
<Cabbage>
form size(350,100), caption("Strobe Bar Model")
button bounds( 10,10,60,30), text("Off","On"), channel("OnOff")
numberbox bounds( 80, 5,70,30), range(0,1000,6,1,0.0001), channel("SHrate"), text("S&H.Rate")
numberbox bounds(160, 5,70,30), range(0,1000,20.25,1,0.0001), channel("LFOrate"), text("LFO.Rate")
numberbox bounds(160,40,70,30), range(0,1000,55.0625,1,0.0001), channel("LFOrate2"), text("LFO.Rate 2")
</Cabbage>
<CsoundSynthesizer>
<CsOptions>
-n -dm0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 16
nchnls = 2
0dbfs = 1
giTri ftgen 0,0,4097,7,0,2048,1,2048,0
giSqu ftgen 0,0,4097,7,1,2048,1,0,0,2048,0
instr 1
kOnOff chnget "OnOff"
gkSHrate chnget "SHrate"
gkLFOrate chnget "LFOrate"
gkLFOrate2 chnget "LFOrate2"
if trigger(kOnOff,0.5,0)==1 then
event "i",2,0,-1
elseif trigger(kOnOff,0.5,1)==1 then
turnoff2 2,0,0
endif
endin
instr 2
ktrig metro gkSHrate
aNdx poscil3 5.999, gkLFOrate, giTri
aNdx samphold aNdx, ktrig
kNdx downsamp aNdx
aamp poscil3 1, gkLFOrate2, giSqu
aamp samphold (aamp*0.7) + 0.3, ktrig
kamp downsamp aamp
schedkwhen ktrig,0,0,3,0,0.1,int(kNdx),kamp,kNdx
endin
giStiffs[] fillarray 37, 50, 60, 70, 80, 90
giDurs[] fillarray 2, 1.8, 1.6, 1.4, 1.2, 1
instr 3
p3 = giDurs[p4]
iK = giStiffs[p4]
iK = 37*(1+(2/(p6+1)))
asig barmodel 2, 2, iK, 0.5, 0, p3, 0.4+rnd(0.2), 2000*p5, 0.07
outs asig, asig
endin
</CsInstruments>
<CsScore>
i 1 0 [3600*24*365]
</CsScore>
</CsoundSynthesizer>
II. Pendulum Waves
The pendulum waves experiment is a favourite of physics department open days. It takes an array of pendulums of decreasing lengths, all connected along a single axle, which are released into motion from the same initial angle at the same time. The magic of the effect is provided by the sequence of patterns that emerge and dissolve unexpectedly as various members of the set of pendulums move into and out of phase at various times during the process. The caveat is that the lengths of the pendulums need to be carefully chosen to ensure the most visible results, but these are relatively easy to calculate. Several demonstrations of the pendulum waves effect can be found on YouTube, here is one of them:
If we ignore the effects of air resistance and friction at the pivot, the physics of a pendulum are relatively simple. It is initially surprising to note that the mass of the bob is irelevant in defining the period of the swing. This irrelevance of mass, once air resistance is removed, was first proposed by the Italian Renaissance scientist Galileo Galilei and was finally confirmed experimentally on the Moon when astronaut David Scott demonstrated a feather and a hammer released at the same time, falling at the same rate.
The formula for calculating the period (time to complete an oscillation) of a pendulum of a known length is:
Where L is the length of the pendulum and g is acceleration due to gravity. If we have a desired period and want to know the length of pendulum that will create this, we can derive the following equation:
For the pendulum waves effect we are interested in creating a sequence of pendulums that are all initially all in sync and only again after 1 minute, therefore we want to replace period with frequency in swings per minute. Frequency is simply the reciprocal of period so we can derive the following equation:
Now we simply need to replace f with an integer number of swings per minute for each of our pendulums. g, or acceleration due to gravity, can be replaced with the approximation, 9.81. A typical set of values for twelve pendulums might be:
|
Swings per minute |
60 |
59 |
58 |
57 |
56 |
55 |
54 |
53 |
52 |
51 |
50 |
49 |
|
Length (m) |
0.248 |
0.257 |
0.266 |
0.275 |
0.285 |
0.296 |
0.307 |
0.318 |
0.331 |
0.344 |
0.358 |
0.373 |
We can use this data to create animations of pendulums using Cabbage widgets. The phase of each pendulum is defined using a sine wave oscillator and trigonometry is used to calculate the positions of pendulums at any particular point in time. A simple sonification is applied whereby each pendulum triggers a sound when it passes through the lowermost point of its travel. In order to sonically identify each pendulum, the pitches produced are proportional to the length of the pendulums.
; Example06.csd
<Cabbage>
form size(300,200), guirefresh(16), colour("white")
image bounds(150,0,1,165), colour(200,200,200), shape("sharp")
image bounds(0,0,0,0), widgetarray("bob",12), shape("ellipse"), colour("black")
numberbox bounds(5,170,60,30), text("Time"), channel("time"), range(-100000,10000,0,1,0.01), colour("white"), textcolour("black"), fontcolour("black")
</Cabbage>
<CsoundSynthesizer>
<CsOptions>
-n -dm0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 16
nchnls = 2
0dbfs = 1
instr 1
gkRefresh metro 32
endin
instr 2
iMToPix init 400 ; scaling sizes to pixels
ix_OS = 150 ; x position offset
iRad = 7 ; radius of bob (visual only)
iInitAngle = 75 ; initial angle from which to swing
iInitAngle /= 90 ; initial angle in radians
iSpeed = 0.3 ; speed modulation of the process: 1=normal <1=slowed down etc.
iDamp = 0.001 ; amount of damping experience by the pendulums
iL = ((60/(2*$M_PI*p4))^2)*9.81 ; calculate length of pendulum
iT = 2 * $M_PI * sqrt(iL/9.81) * (1/iSpeed) ; period of a pendulum swing - dependent upon pendulum length but not mass
kamp init iInitAngle ; set initial angle
kamp = kamp / (1+(iDamp/kr)) ; amplitude of swing, decreased by damping coefficient upon each k-cycle
kphs poscil kamp,1/iT,-1,0.75 ; pendulum phase
ktime init 0 ; initialise elapsed time counter
if metro:k(8)==1 then ; update elapsed time widget 8 times per second
chnset ktime,"time" ; send new time value to numberbox widget
endif
ktime += iSpeed/kr ; increment time (account for speed modulation)
Sident sprintf "bob_ident%d",p5
if gkRefresh==1 then ; if a (graphic) refresh trigger is received...
kx_pix = sin($M_PI*kphs*0.5)*iL*iMToPix ; use trig to calculate x position for bob
ky_pix = cos($M_PI*kphs*0.5)*iL*iMToPix ; use trig to calculate y position for bob
Smsg sprintfk "bounds(%d,%d,%d,%d)", kx_pix + ix_OS - (iRad*0.5), ky_pix -(iRad*0.5), iRad, iRad ; generate message for new position of widget
chnset Smsg, Sident ; send new position message to widget
endif
if trigger(kphs,0,2)==1 && timeinstk()!=1 then ; if pendulum is crossing the sound trigger line
icps = cpsmidinn(20+(p5*6.717)) ; derive a sound frequency value from the length of the pendulum
event "i",3,0,440/icps,icps ; trigger a sound event
endif
SKIP:
endin
instr 3 ; a simple sound 'ping'
aenv expon 1,p3,0.001
iamp = 1/octcps(p4)
asig poscil iamp*aenv,p4
asig *= poscil:a(1,300)
outs asig,asig
endin
</CsInstruments>
<CsScore>
i 1 0 3600
i 2 0 3600 49 1
i 2 0 3600 50 2
i 2 0 3600 51 3
i 2 0 3600 52 4
i 2 0 3600 53 5
i 2 0 3600 54 6
i 2 0 3600 55 7
i 2 0 3600 56 8
i 2 0 3600 57 9
i 2 0 3600 58 10
i 2 0 3600 59 11
i 2 0 3600 60 12
</CsScore>
</CsoundSynthesizer>
Again it can be observed how the pendulums move in and out of phase with one another and at different locations in the swings, sometimes in pairs, sometimes in threes, fours or sixes but we only get fleeting impressions of this in this demonstration. If we replace the oscillator that defines the swing phases with just a calculation of that pendulum’s phase according to a given time since the pendulums were released, we can examine with more precision the stages of coherence that the set of pendulums goes through before they all resynchronise after 1 minute. The following example allows the user to increment time manually, go backwards in time, or to jump to a specific time. Whenever this time value changes the pendulums are set to their appropriate locations.
; Example07.csd
<Cabbage>
form size(300,200), guirefresh(32), text("Pendulum"), colour("white")
image bounds(0,0,0,0), widgetarray("weight",12), shape("ellipse"), colour("black")
button bounds( 0,185,20,15), text("-","-"), channel("dec"), latched(0), colour:0("white"), colour:1("white"), fontcolour:0("black"), fontcolour:1("black")
numberbox bounds( 20,170,70,30), channel("time"), range(0,10000,0,1,0.0001), text("time"), colour("white"), textcolour("black"), fontcolour("black")
button bounds( 90,185,20,15), text("+","+"), channel("inc"), latched(0), colour:0("white"), colour:1("white"), fontcolour:0("black"), fontcolour:1("black")
</Cabbage>
<CsoundSynthesizer>
<CsOptions>
-n -dm0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 16
nchnls = 2
0dbfs = 1
gisine ftgen 0,0,4096,9,1,1,270
giMToPix init 400 ; scaling sizes to pixels
gix_OS = 150 ; x position offset
giRad = 7 ; radius of weight (visual only)
giDamp = 0 ; damping (0=no_damping 1=maximum_damping)
giInitAngle = 75
giInitAngle /= 90
instr 1
gkRefresh metro 16
gktime chnget "time"
kdec chnget "dec"
kinc chnget "inc"
if kdec==1 then
chnset limit(gktime-0.0001,0,10000),"time"
endif
if kinc==1 then
chnset limit(gktime+0.0001,0,10000),"time"
endif
endin
instr 2
ilen = (((60/p4)/(2*$M_PI))^2)*9.81 ; calculate length of pendulum
kamp init giInitAngle
kamp = kamp / (1+(giDamp/kr))
kphs = gktime*(p4/60)
kphs tablei kphs,gisine,1,0,1
kphs *= kamp
Sident sprintf "weight_ident%d",p5
kx_pix = sin($M_PI*kphs*0.5)*ilen*giMToPix
if gkRefresh==1 then
kx_pix = sin($M_PI*kphs*0.5)*ilen*giMToPix
ky_pix = cos($M_PI*kphs*0.5)*ilen*giMToPix
Smsg sprintfk "bounds(%d,%d,%d,%d)", kx_pix+gix_OS-(giRad*0.5), ky_pix-(giRad*0.5), giRad, giRad
chnset Smsg, Sident
endif
endin
</CsInstruments>
<CsScore>
i 1 0 3600
i 2 0 3600 49 1
i 2 0 3600 50 2
i 2 0 3600 51 3
i 2 0 3600 52 4
i 2 0 3600 53 5
i 2 0 3600 54 6
i 2 0 3600 55 7
i 2 0 3600 56 8
i 2 0 3600 57 9
i 2 0 3600 58 10
i 2 0 3600 59 11
i 2 0 3600 60 12
</CsScore>
</CsoundSynthesizer>
Figure 4 below illustrates the most obvious phases of coherence through which the pendulums pass in a minute. The timings, from when initially released, at which these occur are shown in the bottom left corner of each frame.
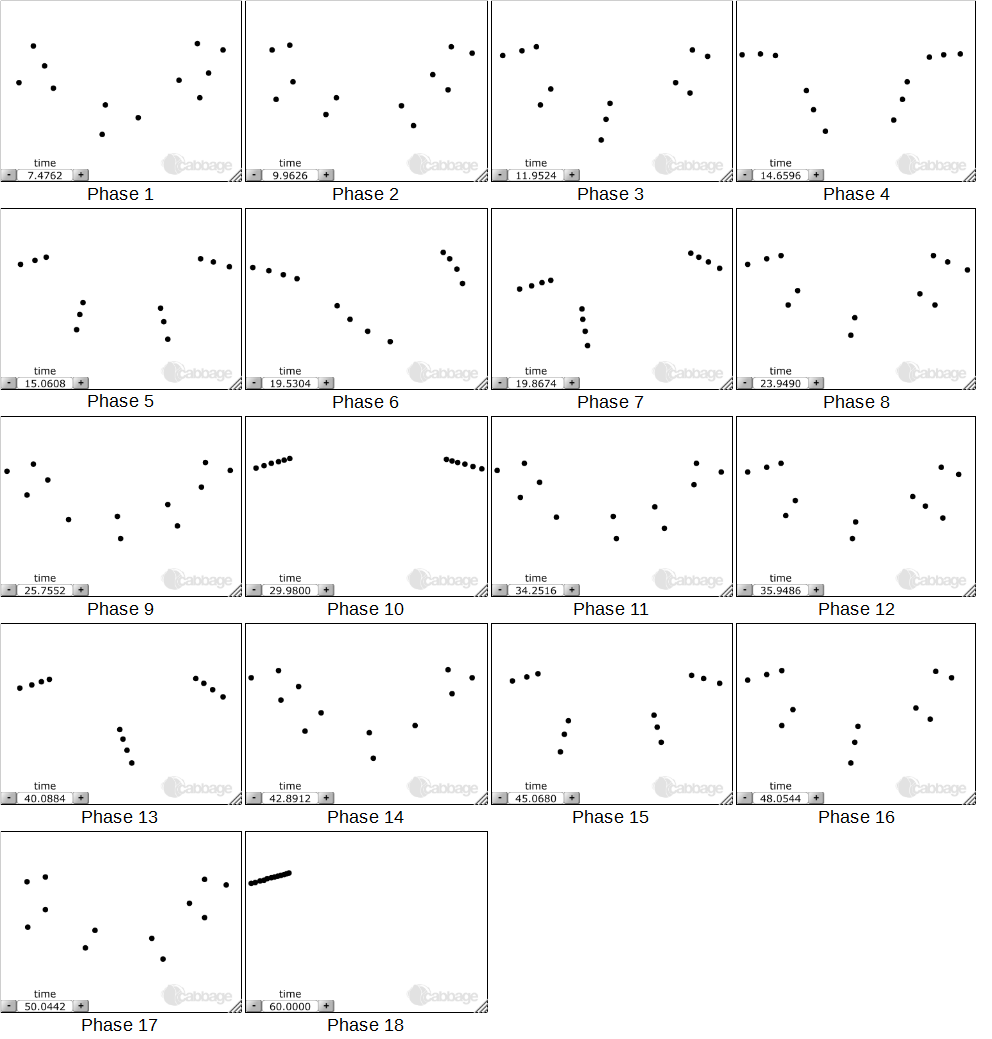
Figure 4. Phases of pendulum coherence.
During phase 1 at around 7.5 seconds, 4 pairs of pendulums emerge, at around 10 seconds, 6 pairs of pendulums emerge, at around 12 seconds 2 sets of 3 pendulums and 3 sets of 2 pendulums emerge and so on.
With a greater understanding of the influencing factors upon the formation of patterns within the set of pendulums, we can start to manipulate the various parameters of the original model to explore what further possiblilities there might be for pattern generation in Csound. The final example (Figure 5 and Example08.csd below) adds many more options for real-time user interaction. The speed factor can now be modulated from within the GUI. If "Hold Pattern" is activated, the current pattern is maintained, i.e. all oscillation periods will be the same regardless of pendulum length. We can set the initial phase of all pendulums using "Init.Angle" although employment of changed values will require hitting "Restart". "Trig.Angle" sets the phase location at which pendulums will trigger a sound—this is no longer fixed at the lowest point of their swings—and this setting is reflected in the position of a grey line, as well as sonically. "Damping" allows for setting the amount of damping the pendulums will experience as they swing. If this is zero, all pendulums will swing indefinitely. "Size Scale" is merely used to scale up or down the visual representation of the swinging pendulums—this is useful if they swing beyond the boundaries of the panel. The frequency of each pendulum can also be modified from the GUI. This will be reflected in a changing length of that pendulum and this will happen in real-time so no restart of the process is required.
With these added options the instrument becomes an effective machine for real-time pattern generation. Controlling the pattern with these abstracted input controls suggests a form of algorithmic composition. Compositional decisions can be effected by, for example, freezing an emerging pattern that is deemed desirable using "Hold Pattern". Patterns can be revisited by reversing time through giving "Speed" a negative value. The greatest scope is presented by the ability to set each individual pendulum to any frequency value. This opens up the possibility of setting up multiple sub-groupings of pendulums: a polyphony of pendulum-waves sets.
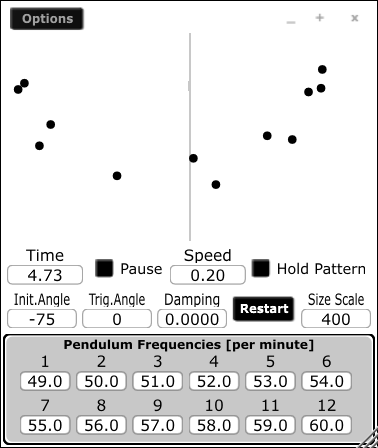
Figure 5. Pendulum waves Cabbage interface.
; Example08.csd
<Cabbage>
form size(300,330), guirefresh(16), text("Pendulum"), colour("white")
image bounds(150,0,1,165), colour(200,200,200), shape("sharp"), rotate(0,1,1), identchannel("TrigAngleID")
image bounds(0,0,0,0), widgetarray("bob",12), shape("ellipse"), colour("black")
numberbox bounds(5,170,60,30), text("Time"), channel("time"), range(-100000,10000,0,1,0.01), colour("white"), textcolour("black"), fontcolour("black")
checkbox bounds(75,180,60,15), text("Pause"), channel("pause"), fontcolour("black")
numberbox bounds(135,170,60,30), text("Speed"), channel("speed"), range(-10,10,0.2,1,0.01), colour("white"), textcolour("black"), fontcolour("black")
checkbox bounds(200,180,90,15), text("Hold Pattern"), channel("sync"), fontcolour("black")
numberbox bounds(5,205,55,30), text("Init.Angle"), channel("InitAngle"), range(-90,90,-75,1,1), colour("white"), textcolour("black"), fontcolour("black")
numberbox bounds(65,205,55,30), text("Trig.Angle"), channel("TrigAngle"), range(-90,90,0,1,1), colour("white"), textcolour("black"), fontcolour("black")
numberbox bounds(125,205,55,30), text("Damping"), channel("Damping"), range(0,0.1,0,1,0.0001), colour("white"), textcolour("black"), fontcolour("black")
button bounds(185,210,50,20), text("Restart","Restart"), channel("Restart")
numberbox bounds(240,205,55,30), text("Size Scale"), channel("MToPix"), range(10,5000,400,1,1), colour("white"), textcolour("black"), fontcolour("black")
image bounds( 2,240,296,88), colour(200,200,200), outlinecolour("black"), outlinethickness(2), shape("rounded")
label bounds( 2,242,296,12), text("Pendulum Frequencies [per minute]"), fontcolour("black")
numberbox bounds( 15,255,40,30), text("1"), channel("F1"), range(10,500,49,1,0.1), colour("white"), textcolour("black"), fontcolour("black")
numberbox bounds( 60,255,40,30), text("2"), channel("F2"), range(10,500,50,1,0.1), colour("white"), textcolour("black"), fontcolour("black")
numberbox bounds(105,255,40,30), text("3"), channel("F3"), range(10,500,51,1,0.1), colour("white"), textcolour("black"), fontcolour("black")
numberbox bounds(150,255,40,30), text("4"), channel("F4"), range(10,500,52,1,0.1), colour("white"), textcolour("black"), fontcolour("black")
numberbox bounds(195,255,40,30), text("5"), channel("F5"), range(10,500,53,1,0.1), colour("white"), textcolour("black"), fontcolour("black")
numberbox bounds(240,255,40,30), text("6"), channel("F6"), range(10,500,54,1,0.1), colour("white"), textcolour("black"), fontcolour("black")
numberbox bounds( 15,290,40,30), text("7"), channel("F7"), range(10,500,55,1,0.1), colour("white"), textcolour("black"), fontcolour("black")
numberbox bounds( 60,290,40,30), text("8"), channel("F8"), range(10,500,56,1,0.1), colour("white"), textcolour("black"), fontcolour("black")
numberbox bounds(105,290,40,30), text("9"), channel("F9"), range(10,500,57,1,0.1), colour("white"), textcolour("black"), fontcolour("black")
numberbox bounds(150,290,40,30), text("10"), channel("F10"), range(10,500,58,1,0.1), colour("white"), textcolour("black"), fontcolour("black")
numberbox bounds(195,290,40,30), text("11"), channel("F11"), range(10,500,59,1,0.1), colour("white"), textcolour("black"), fontcolour("black")
numberbox bounds(240,290,40,30), text("12"), channel("F12"), range(10,500,60,1,0.1), colour("white"), textcolour("black"), fontcolour("black")
</Cabbage>
<CsoundSynthesizer>
<CsOptions>
-n -dm0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 16
nchnls = 2
0dbfs = 1
instr 1 ; start pendulums
gkRefresh metro 32 ; refresh rate
gkFreqs[] init 12 ; array of pendulum frequency values
gkRestart chnget "Restart" ; manual restart trigger
gkMToPix chnget "MToPix" ; scaling sizes to pixels
gkFreqs[0] = chnget:k("F1")
gkFreqs[1] = chnget:k("F2")
gkFreqs[2] = chnget:k("F3")
gkFreqs[3] = chnget:k("F4")
gkFreqs[4] = chnget:k("F5")
gkFreqs[5] = chnget:k("F6")
gkFreqs[6] = chnget:k("F7")
gkFreqs[7] = chnget:k("F8")
gkFreqs[8] = chnget:k("F9")
gkFreqs[9] = chnget:k("F10")
gkFreqs[10] = chnget:k("F11")
gkFreqs[11] = chnget:k("F12")
gkL12 = ((60/(2*$M_PI*gkFreqs[11]))^2)*9.81 ; length of the last pendulum
iCount = 0
loop:
event_i "i",2+(iCount/100),0,3600,iCount
loop_lt iCount,1,12,loop
endin
instr 2 ; a pendulum
if changed(gkRestart)==1 then ; if a restart trigger has been received
reinit RESTART ; reinitialise from label
endif
RESTART:
ix_OS = 150 ; x position offset
iRad = 7 ; radius of bob (visual only)
iInitAngle chnget "InitAngle" ; initial angle of from which swing begins
iInitAngle /= -90 ; in radians
kSpeed chnget "speed" ; speed 1=normal, <1=slow_motion etc.
kpause chnget "pause" ; pause motion if '1'
ksync chnget "sync" ; if '1' all pendulums adopt the same frequency, i.e. pattern is held and repeated
kTrigAngle chnget "TrigAngle" ; angle at which sounds are triggered
kDamping chnget "Damping" ; amount of amplitude damping the pendulums experience
if changed(kTrigAngle)==1 then ; if sound trigger angle is changed...
Smsg sprintfk "rotate(%f,1,1)",-kTrigAngle/90 *1.57 ; create a new string for the Cabbage line widget
chnset Smsg, "TrigAngleID" ; send string to the widget to update its appearance
endif
kFreq = gkFreqs[p4] ; read frequency value for this pendulum from array
kL = ((60/(2*$M_PI*kFreq))^2)*9.81 ; calculate length of pendulum
if kpause==1 kgoto SKIP ; if pause button is on skip all further processes in this instrument
if ksync==0 then ; is sync button is off (follow normal behaviour)
kPeriod = 2 * $M_PI * sqrt(kL/9.81) * (1/kSpeed) ; period of a pendulum swing - dependent upon pendulum length but not mass
else
kPeriod = 2 * $M_PI * sqrt(gkL12/9.81) * (1/kSpeed) ; sync is on: all pendulums use the same length value
endif
kamp init iInitAngle ; amplitude initialised according to initial angle of swing set by widget
kamp = kamp / (1+(kDamping/kr)) ; amplit; update elapsed time widget 8 times per secondude of swing, decreased by damping coefficient upon each k-cycle
kphs poscil kamp,1/kPeriod,-1,0.75 ; pendulum phase
ktime init 0 ; initialise elapsed time counter
if metro:k(8)==1 then
chnset ktime,"time" ; send new time value to numberbox widget
endif
if ksync==0 then ; if sync is off, (i.e. in sync-on mode, freeze elapsed time counter)
ktime += kSpeed/kr ; increment time (account for speed modulation)
endif
Sident sprintf "bob_ident%d",p4+1 ; generate a string for the ident name for this particular pendulum bob
if gkRefresh==1 then ; if a (graphic) refresh trigger is received...
kx_pix = sin($M_PI*kphs*0.5)*kL*gkMToPix ; use trig to calculate x position for bob
ky_pix = cos($M_PI*kphs*0.5)*kL*gkMToPix ; use trig to calculate y position for bob
Smsg sprintfk "bounds(%d,%d,%d,%d)", kx_pix + ix_OS - (iRad*0.5), ky_pix -(iRad*0.5), iRad, iRad ; generate message for new position of widget
chnset Smsg, Sident ; send new position message to widget
endif
if trigger(kphs,kTrigAngle/90,2)==1 && timeinstk()!=1 then ; if pendulum is crossing the sound trigger line
icps = cpsmidinn(20+((p4+1)*6.717)) ; derive a sound frequency value from the length of the pendulum
event "i",3,0,440/icps,icps ; trigger a sound event
endif
SKIP:
endin
instr 3 ; a sound ping
aenv expon 1,p3,0.001
iamp = 1/octcps(p4)
asig poscil iamp*aenv,p4
asig *= poscil:a(1,300)
outs asig,asig
endin
</CsInstruments>
<CsScore>
i 1 0 3600
</CsScore>
</CsoundSynthesizer>
Conclusion
The ability to generate complex musical patterns that exhibit clear coherence, but through an abstracted and simplified interaction with that process, is an appealing prospect. It can be a compositional inhibition to have to manually define the start time and all ancilliary parameters for each and every sound event desired, the use of an abstracted machine for this task can streamline note generation and can spawn pleasantly unexpected results. Ignoring more conventional approaches such as loop sequencers and piano roll sequencers leads to a new kind of music, and in this area Csound excels. The visual analogues that were used as starting points for these models, and that were deployed using Cabbage’s facilities for manipulating its widgets, are ultimately superfluous in the final music making, but their presence provides a confirmation of the mechansim and even anticipation of imminent sound patterns. These examples stop at the point at which the visual manifestation has been transmuted into a musical analogue, but the obvious direction in which to proceed would be to release the focus with respect to the visual source and pursue purely musical avenues of interest.
References
[1] Rory Walsh, "Cabbage", A framework for software development. [Online] Available: http://cabbageaudio.com/ [Accessed March 10, 2016].
[2] "The Wagon-wheel effect." [Online] Available: https://en.wikipedia.org/wiki/Wagon-wheel_effect [Accessed January 26th, 2016].
[3] "Pendulum Waves." Harvard Natural Sciences Lecture Demonstrations. [Online] Available: https://www.youtube.com/watch?v=yVkdfJ9PkRQ&feature=youtu.be [Accessed January 26th, 2016].