Introduction
This article briefly covers aspects of bandlimiting to avoid aliasing while employing a "rich" sound source such as a sawtooth wave. Multiple lookup tables are employed. Examples of changes in tone color are also provided employing bandlimiting techniques. Solutions for slow compilation times employing Midi pitch numbers instead of frequencies in Hz are put forward. A brief discussion, and examples of employing a filter are included. Finally a small graphical user interface example to control bandlimited frequency, timbre, and amplitude is included in the article below as well as code to covert from MIDI to frequencies in Hz and vice versa, and a UDO to print harmonic partial frequencies.Non-Bandlimited Sine
The sine wave, represented by a single fundamental strength and amplitude in the GEN10 routine, can be swept from 1 Hertz to the half sample rate of a Csound file header without aliasingf1 0 512 10 1There is no call for bandlimiting, in this case, due to the fact that the sine is a single fundamental and will not cause aliasing due to overtones which are above one-half the sampling rate. (Ex1.csd, Non-Bandlimited Sine)
kenv linseg 1, p3, sr/2 asig oscili 5000, kenv, 1
Non-Bandlimited Sawtooth and Aliasing
As soon as the same frequency sweep uses a rich sawtooth wave as sound source, we can quickly hear the result of foldover or aliasing. This is due to the higher harmonics generated from the sawtooth wave.(Ex2.csd, Non-Bandlimited Aliased Sawtooth)f2 0 16384 7 1 16384 -1An oscillator using a "rich" wave source, such as a sawtooth wave, will frequently provide a bandlimited option. Band limiting the "rich" sound source is one alternative for using such a sound source throughout a large frequency range. (See Bidule, http://www.plogue.com/ , or Open Sound World, http://osw.sourceforge.net/ ) Csound's VCO opcode is also an implementation of a band limited, analog modeled oscillator based on integration of band limited impulses. It features sawtooth, square, and triangle waveforms.
kenv linseg 1, p3, sr/2 asig oscili 5000, kenv, 2
Generating Bandlimited Tables using Frequencies in Hertz
One solution to work against aliasing and attempting to preserve harmonic content is band limiting across the frequency spectrum.With GEN30, one is able to able to control the harmonic content (imaxh). Thus it is possible to generate one table for each frequency up to half sampling rate, then employ the tables as band limiting. (Ex3.csd, Bandlimited Tables using frequencies in Hz)
/* sawtooth wave */ i_ ftgen 30000, 0, 16384, 7, 1, 16384, -1 /* generate bandlimited sawtooth waves for ALL FREQS up 1/2 SR */ i0 = 0 loop1: imaxh = (sr/2) / i0 i_ ftgen i0, 0, 4096, -30, 30000, 1, imaxh ;print imaxh i0 = i0 + 1 if (i0 < sr/2) igoto loop1
Generating Bandlimited Tables using MIDI
Although the approach above works well, it is time consuming to generate the large numbers of tables required, and thus not very effective for realtime applications. Also only frequencies as integers were generated. It would be even more time consuming, and memory intensive to generate a table for each frequency if including floating point numbers. That would be for all frequencies, not just the twelve equal tempered pitches.If table generation time is a factor, then perhaps generating tables for midi notes might prove more effective (Ex4.csd, Bandlimited Tables using Midi Pitch Numbers). The i-time loop below comes from Istvan Varga's example for the OscBnk opcode, from the Csound Users Manual, in which he includes bandlimited sawtooth waves.
/* Create a rich sawtooth wave */ i_ ftgen 30000, 0, 16384, 7, 1, 16384, -1 /* generate bandlimited sawtooth waves for MIDI pitch nums */ i0 = 0 loop1: imaxh = sr / (2 * 440.0 * exp (log(2.0) * (i0 - 69) / 12)) i_ ftgen i0, 0, 4096, -30, 30000, 1, imaxh i0 = i0 + 1 if (i0 < 127.5) igoto loop1
But not everyone deals with discrete equal tempered pitches produced by midi note numbers, thus a compromise solution may be employed to generate band limited harmonic content tables for midi note numbers, and to convert midi note numbers back to frequencies in Hz for the sound generating opcode. In this case the harmonic content does not change as rapidly, but still provides the effect of avoiding aliasing. The use of midi pitch numbers as table numbers, although time saving, however does not provide the smoothest changes between tables during sweeps since each table covers a range of frequencies (See the Csound Manual, "Appendix A.Pitch Conversion"). (Ex5.csd, Convert from Midi to frequencies in Hz and vice versa)
/* CONVERT MIDI NUMBER TO FREQ in Hz */ ;f(n) = 440 * 2exp((n-69)/12) ;convert n = midi pitch num to freq in Hz ;i0 = 0 ;loop1: ;icps = 440.0 * exp(log(2.0) * (i0 - 69.0) / 12.0) ;print icps ;i0 = i0 + 1 ;if (i0 < 127.5) igoto loop1 /* CONVERT frequencies in Hz NUMBER TO MIDI */ ;n = 12 * (log(f/220)/log(2))+57 ;convert freq to midi num i0 = 8 loop1: imidi = 12 * (log(i0/220)/log(2))+57 imidi = round (imidi) print i0, imidi i0 = i0 + 1 if (i0 <= sr/2) igoto loop1
Timbre Sweeps on One Pitch
If we have a particular frequency or midi note number, then range or sweep the timbre based on tables which span from the minimum to the maximum bandwidth allowable for that frequency in order to avoid aliasing, using a relatively low frequency, we are able to perceive a "filtered" effect.An issue associated with a timbral sweep of a complex tone, is as band limiting takes effect for higher fundamental frequencies, thereby reducing the number of harmonics, as the higher harmonics available begin to fall within the range of hearing we begin to notice those harmonics more and more. In other words, for timbral sweeps, when a relatively large number of harmonics are present we tend to "fuse" those with the fundamental to hear a complex sound, but when the number of harmonics is relatively small, and the highest harmonics are within the range of hearing, then we begin to distinguish the individual components of the sound. (Ex6.csd, Bandlimiting using Tablekt with Midi. Note whistling sound)
Regarding our perception of complex tones, Juan Roederer writes about vibrations along the basilar membrane at a position which depends on frequency, and states that a complex tone will give rise to a whole multiplicity of resonance regions, one for each harmonic, and that some overlapping will occur. (Roederer)
Using GEN19 to reduce the number of partials
Exactly how much harmonic content is required in order to perceive sounds as "rich" while moving across the frequency spectrum is somewhat subjective. For example at 100 hertz, we could generate a waveform which will have 220 harmonics before aliasing, where 100 x 220 = 22000, at a sample rate of 44,100 Hz. But because the distance between the partials becomes smaller for higher numbered partials, the total frequency interval covered by a larger number of partials is not much greater than a smaller number of partials which have a significant contribution in terms of amplitude. Additionally we can easily mix and match any contribution of partials, phase, and amplitude using GEN19 arriving at a result which psychoacoustically works as well for us as the 220 harmonics. Or to put it another way, we can skip some partials and still come out with a very close result.The following example employs a low resolution full bandwidth sawtooth wave generated using GEN07, and another limited bandwidth sawtooth using GEN19. (Ex7.csd, Comparing Signals of Different Harmonic Content). The oscil opcode is used to avoid interpolation, and the signals are high-pass filtered to avoid low frequency noise. The limited bandwidth signal compares favorably to the full bandwidth signal.
An interesting aspect about timbre and band limiting is that the higher in frequency we go, the easier it is to approximate timbre between signals employing less partials. This is because the higher we go, the less auditory space there is to work with for harmonic partials as we approach the Nyquist frequency. As we continue higher, everything eventually merges toward a single sine wave. John Chowning states in his paper that in general, the number of partials in a spectrum decreases and the spectral envelope changes shape as pitch increases, that is the centroid of the spectrum shifts toward the fundamental.(Chowning)
But this is not as simple as it seems, for we also know that loudness, spatialization, and phase also provide cues for timbre as well. Chowning's article: "Digital Sound Synthesis, Acoustics, and Perception: A Rich Intersection", covers these aspects in detail.
Also related to the generation of "rich" sounds, Csound's buzz and gbuzz opcodes should be mentioned as signal generating opcodes for which the harmonic content can be controlled at the k-rate. These opcodes are mentioned in Stilson and Smith's article, "Alias-free digital synthesis of classic analog waveforms", regarding pulse trains and Discrete-Summation Formulae (DSF) in the section leading to their more detailed discussion and explanation of pulse trains of sync tones and employing filters as intergrators to control DC components, thereby affecting aliasing of classical waveforms. Eli Brandt's article "Hard Sync Without Aliasing" is also interesting reading for those who may want to read more about complex wave forms from sync tones.
Filtering approach to bandlimiting
Another approach is to try to resolve aliasing problems by tracking and limiting frequency components using a variable bandwidth filter opcode such as Resonx. In Example 8, as the frequency sweeps upward, the spectral content changes from "rich" to "simple" or moving from sawtooth to sine due to the filter's changing bandwidth, thus avoiding aliasing.[Ex8.csd, Bandlimited employing a filter and frequencies in Hz]Miller Puckette includes an example employing a Butterworth filter to reduce the amplitude of partials above the Nyquist, and employs up-sampling to increase the bandwidth of a the signal so that the output will not fold over when it is down-sampled. (Puckette)
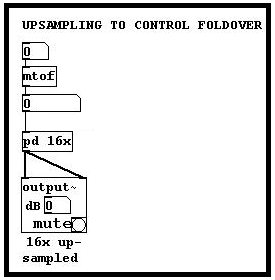
(Fig. 1. J07.oversampling.pd)
Example J07.oversampling.pd, from Puckett's "Theory and Technique of Electronic Music", shows how to use up-sampling to reduce foldover when using a phasor~ object as an audio sawtooth wave. A subpatch, contains the phasor~ object and a three-pole, three-zero Butterworth filter to reduce the amplitudes of partials above the Nyquist frequency of the parent patch so that the output will not fold over when it is down-sampled at the outlet~ object.
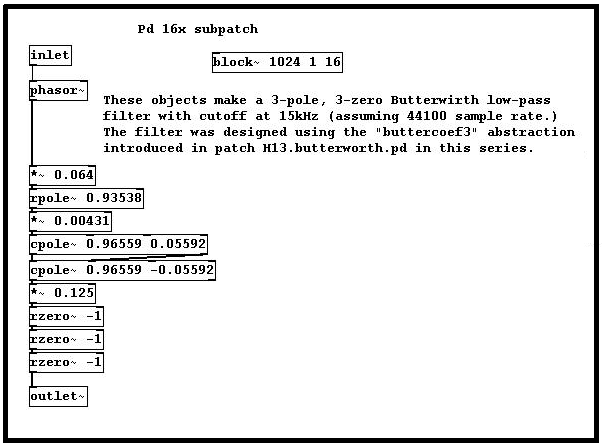
(Fig 2. Pd 16x subpatch)
A simple example of upsampling would be a numerical series (1 2 3 4), where we increase the rate by inserting zeros (1 0 0 2 0 0 3 0 0 4 0 0). In the Butterworth Pd patch, this has the effect of also increasing the 1/2 Sample Rate point or cutoff frequency for possible aliased components, while at the same time decreasing the amplitudes of the higher components due to the 3-pole, 3-zero lowpass design of the filter. On the way back out, the filter's pole coefficients are set to -1, restoring the Nyquist to that of the original sample rate. Again if we have a numerical series ( 1 2 3 4 5 6 7 8 9 10) and downsample or decrease the rate by an integer factor of 2 we could get something like (1 4 7 10).
Returning to the idea of a timbral sweep on one frequency--this can also be accomplished employing a filter. The filter can be implemented to achieve the same impression as employing bandlimiting tables, from Example 6 above, by choosing a frequency, then ranging the bandwidth of the filter from minimum to maximum bandwidth allowable for that frequency in order to avoid aliasing.[Ex9.csd, Bandlimiting using Tablekt with Midi, also Adding a Filter]
Bandlimiting Strategies
A bandlimiting strategy which has worked for me with Csound, is to employ midi pitch numbers to generate tables of bandlimited harmonic content in order to save compile time, and to employ those tables with an opcode such as oscilikt to change tables at the k-rate, but to use frequencies in Hz as the xcps input parameter for oscilikt. The use of a filter is also included for creative applications, employing one which has a k-rate bandwidth input parameter. One could also design a simple FLTK graphical interface with sliders for frequency, timbre, and amplitude. Frequency can be adjusted without aliasing using bandlimited tables, and timbre can be ranged using adjustable bandwidth as related to a particular frequency. (Ex10.csd, an FLTK example)You can download the csd example files here: BandlimitingExs.zip. Also included in the .zip file is a simple UDO utility to print harmonic partial frequencies.
Conclusions
Other aspects of timbre aside, it is more difficult to distinguish timbral differences in higher frequencies due to the fact that there is less harmonic space available with which to work.An interesting phenomenon occurs across the frequency spectrum regarding harmonic content. As the pitch increases, our ears do not distinguish the differences very carefully in harmonic content. In other words, it is difficult to distinguish timbre differences among relatively higher frequencies.
If we use the same frequency, in a relatively low range, and change the harmonic content, we are able to perceive a "filtered" effect, or one sound which is not as rich as the other.
In Csound, table look-up can be combined effectively with filtering to avoid aliasing of complex waveforms.
References
Brandt, Eli. Hard Sync Without Aliasing. (09 Feb 2007).Burk, Phil, et. al. Music and Computers: A Theoretical and Historical Approach. Key College Publishing. Emeryville, California. 2007. www.keycollege.com [a good e-book with interactive java applets and sound file examples]
Chowning, John. Digital Sound Synthesis, Acoustics, and Perception: A Rich Intersection. Proceedings of the COST G-6 Conference on Digital Audio Effects (DAFX-00), Verona, Italy, December 7-9, 2000. (03 Feb 2007).
Csound Users Manual, sourceforge.net/projects/csound also www.csounds.com/ (05 Feb 2007).
Maxim. A Filter Primer. Application Note 733. (02 Feb 2007)
Puckette, Miller. Theory and Technique of Electronic Music . "Strategies for band-limiting sawtooth waves", p. 314. Draft: December 30, 2006. (05 Feb 2007).
Roederer, Juan. Introduction to the Physics and Psychophysics of Music. The English Universities Press Ltd. London. (ISBN- 0-340-18122-2), 1973.
Stilson, T. and J. Smith (1996). Alias-free digital synthesis of classic analog waveforms. (10 Feb 2007).